Transmission T48 to H8A
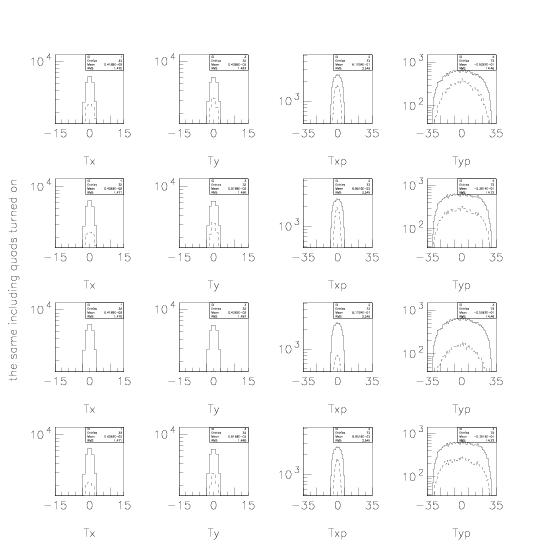
Intrinsic Resolution
One calculates the intrinsic resolution using the matrix elements Rii given e.g. by TRANSPORT. The momentum spread at collimator is given by R16 [mm/%] (R26 being zero). The monochromatic spot size at collimator is given by R11M [mm/mm] and R12 [mm/mrad]. The initial spread at the target is known with x0 [mm] and x0' [mrad]. The monochromatic spot size at collimator is then xc= R11*x0+ R12*x0'. The intrinsic resolution is calculated as R=xc/R16. This simplifies with the assumptions, that the term R11=1 (ideally achievable), R12=0 (focal point), to R=x0/R16. For H8 VLE this results in 0.32 % (0.29 %). (see also P.Coet, N.Doble, "An introduction to the design of high-energy charged particle beams", p.48, CERN/SPS/86-23, 1986)
Muon background
The advantage of using a rather high momentum pion beam from T4 to TlowE is given by the higher pion yield at T4, in less pion decay towards Atlas. The deflection from the trigger chambers is smaller. At a run with 1 GeV pions at ATLAS, the 60 GeV are deflected by 2 mrad, resulting in an offset by 40 mm, so half the lateral chamber size. Muons, which are produced down to a momentum of about 30 GeV/c are deflected even more. The problem of muon background is much reduced by the fact, that the optics placed are optimized for pion focusing through the spectrometer and not for the muons in the straight section. At the same they diverge over a large distance (20 m towards the first trigger SPEC4 and 50 m towards ATLAS itself). A different way of particle production is possible by placing the filter target, , where by this a zero muon background is established, but for sure results in a lower pion intensity at ATLAS
I we assume, that the muons are equally distributed in the momentum spread, and the production is common in each point of phase space, and the beam optics do not sort for momentum as a function of phase space, then we can easily derive the muon distribution in real space from the result of turtle. So far we have also neglected the impact of bend4, which is for sure smaller, as the drift space to the trigger is by a factor 20 shorter.
And we still need to add the scattering by the dump. Seems we are by far on the safe side.
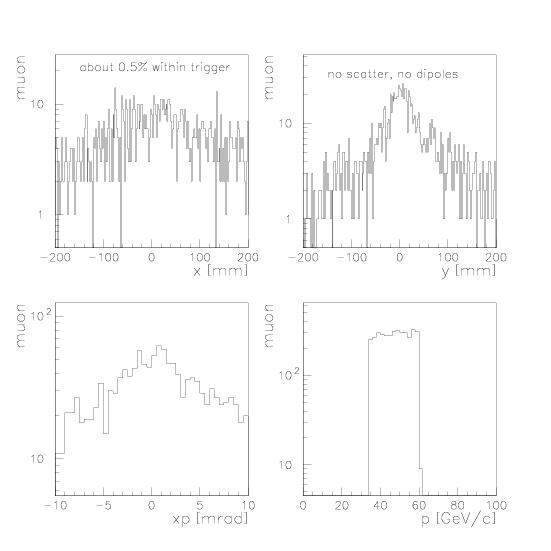
About 300/26000 pions muons are within trigger of spect4, excluded the simulation of the scattering in the dump. THIS IS NOT FOR 1e6 pions at T4, but only for 26000. This was the missing factor. So it results in about 0.5 percent within 10cm x 10cm neglecting deflection by the dipoles and scattering in the dump.
The dead time of a XDWC is about 300 ns. Assuming 10^6 muons (1%) within 4.5 s (SPS spill), this would veto about 0.3 s or 7% of the spill time. The loss in pion intensity is told to be negligible.

